Overview

Say we have a collection of customers with a variety of characteristics such as age, location, and financial history, and we wish to discover patterns and sort them into clusters. Or perhaps we have a set of texts, such as wikipedia pages, and we wish to segment them into categories based on their content. This is the world of unsupervised learning, called as such because we are not guiding, or supervising, the pattern discovery by some prediction task, but instead uncovering hidden structure from unlabeled data. Unsupervised learning encompasses a variety of techniques in machine learning, from clustering to dimension reduction to matrix factorization. We’ll explore the fundamentals of unsupervised learning and implement the essential algorithms using scikit-learn and scipy. We will explore how to cluster, transform, visualize, and extract insights from unlabeled datasets, and end the session by building a recommender system to recommend popular musical artists.

Libraries

from sklearn import datasets
from sklearn.cluster import KMeans
from sklearn.preprocessing import (StandardScaler, 
                                   Normalizer, 
                                   normalize, 
                                   MaxAbsScaler)
from sklearn.pipeline import make_pipeline
from sklearn.manifold import TSNE
from sklearn.decomposition import (PCA, 
                                   TruncatedSVD, 
                                   NMF)
from sklearn.feature_extraction.text import TfidfVectorizer

import numpy as np
import pandas as pd

from scipy.cluster.hierarchy import (linkage, 
                                     dendrogram, 
                                     fcluster)
from scipy.stats import pearsonr
from scipy.sparse import csr_matrix

import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
plt.style.use("ggplot")

import warnings
warnings.filterwarnings("ignore", message="numpy.ufunc size changed")
warnings.filterwarnings("ignore", message="invalid value encountered in sign")

Clustering for dataset exploration

Exploring how to discover the underlying groups (or “clusters”) in a dataset. We’ll be clustering companies using their stock market prices, and distinguishing different species by clustering their measurements.

Unsupervised Learning

Unsupervised learning

Unsupervised learning finds patterns in data

E.g. clustering customers by their purchases

Compressing the data using purchase patterns (dimension reduction)

Supervised vs unsupervised learning

Supervised learning finds patterns for a prediction task

E.g. classify tumors as benign or cancerous (labels)

Unsupervised learning finds patterns in data

… but without a specific prediction task in mind

Iris dataset

Measurements of many iris plants {% fn 1 %}

3 species of iris: setosa, versicolor, virginica

Petal length, petal width, sepal length, sepal width (the features of the dataset)

Iris data is 4-dimensional

Iris samples are points in 4 dimensional space

Dimension = number of features

Dimension too high to visualize!

… but unsupervised learning gives insight

k-means clustering

Finds clusters of samples

Number of clusters must be specified

Implemented in sklearn (“scikit-learn”)

Cluster labels for new samples

New samples can be assigned to existing clusters

k-means remembers the mean of each cluster (the “centroids”)

Finds the nearest centroid to each new sample

Scatter plots

Scatter plot of sepal length vs petal length

Each point represents an iris sample

Color points by cluster labels

PyPlot (matplotlib.pyplot) TODO: add scatter plot

iris = datasets.load_iris()
iris.keys()

dict_keys(['data', 'target', 'frame', 'target_names', 'DESCR', 'feature_names', 'filename'])

samples = iris.data
samples[:5]

array([[5.1, 3.5, 1.4, 0.2],
       [4.9, 3. , 1.4, 0.2],
       [4.7, 3.2, 1.3, 0.2],
       [4.6, 3.1, 1.5, 0.2],
       [5. , 3.6, 1.4, 0.2]])

k-means clustering with scikit-learn

model = KMeans(n_clusters=3)
model.fit(samples)

KMeans(n_clusters=3)

labels = model.predict([[5.8, 4. , 1.2, 0.2]])
labels

array([1])

Cluster labels for new samples

new_samples = [[ 5.7,4.4,1.5,0.4] ,[ 6.5,3. ,5.5,1.8] ,[ 5.8,2.7,5.1,1.9]]
model.predict(new_samples)

array([1, 2, 0])

Scatter plots

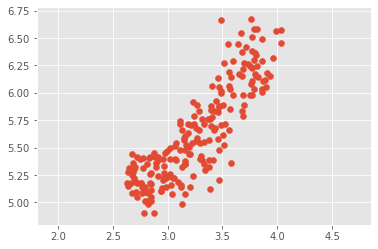
labels_iris = model.predict(samples)

xs_iris = samples[:,0]
ys_iris = samples[:,2]
_ = sns.scatterplot(xs_iris, ys_iris, hue=labels_iris)
plt.show()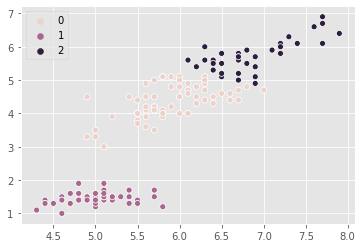

points = pd.read_csv("datasets/points.csv").values
points[:5]

array([[ 0.06544649, -0.76866376],
       [-1.52901547, -0.42953079],
       [ 1.70993371,  0.69885253],
       [ 1.16779145,  1.01262638],
       [-1.80110088, -0.31861296]])

xs_points = points[:,0]
ys_points = points[:,1]
_ = sns.scatterplot(xs_points, ys_points)
plt.show()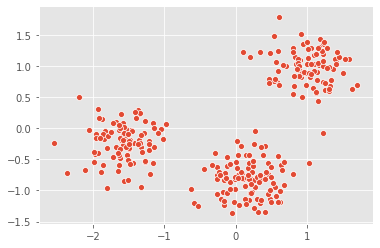

There are three clusters

Clustering 2D points

From the scatter plot we saw that the points seem to separate into 3 clusters. we’ll now create a KMeans model to find 3 clusters, and fit it to the data points. After the model has been fit, we’ll obtain the cluster labels for some new points using the .predict() method.

new_points = pd.read_csv("datasets/new_points.csv").values
new_points[:5]

array([[ 0.40023333, -1.26544471],
       [ 0.80323037,  1.28260167],
       [-1.39507552,  0.05572929],
       [-0.34119268, -1.07661994],
       [ 1.54781747,  1.40250049]])

# Create a KMeans instance with 3 clusters: model
model_points = KMeans(n_clusters=3)

# Fit model to points
model_points.fit(points)

# Determine the cluster labels of new_points: labels
labels_points = model_points.predict(new_points)

# Print cluster labels of new_points
print(labels_points)

[0 2 1 0 2 0 2 2 2 1 0 2 2 1 1 2 1 1 2 2 1 2 0 2 0 1 2 1 1 0 0 2 2 2 1 0 2
 2 0 2 1 0 0 1 0 2 1 1 2 2 2 2 1 1 0 0 1 1 1 0 0 2 2 2 0 2 1 2 0 1 0 0 0 2
 0 1 1 0 2 1 0 1 0 2 1 2 1 0 2 2 2 0 2 2 0 1 1 1 1 0 2 0 1 1 0 0 2 0 1 1 0
 1 1 1 2 2 2 2 1 1 2 0 2 1 2 0 1 2 1 1 2 1 2 1 0 2 0 0 2 1 0 2 0 0 1 2 2 0
 1 0 1 2 0 1 1 0 1 2 2 1 2 1 1 2 2 0 2 2 1 0 1 0 0 2 0 2 2 0 0 1 0 0 0 1 2
 2 0 1 0 1 1 2 2 2 0 2 2 2 1 1 0 2 0 0 0 1 2 2 2 2 2 2 1 1 2 1 1 1 1 2 1 1
 2 2 0 1 0 0 1 0 1 0 1 2 2 1 2 2 2 1 0 0 1 2 2 1 2 1 1 2 1 1 0 1 0 0 0 2 1
 1 1 0 2 0 1 0 1 1 2 0 0 0 1 2 2 2 0 2 1 1 2 0 0 1 0 0 1 0 2 0 1 1 1 1 2 1
 1 2 2 0]

We’ve successfully performed k-Means clustering and predicted the labels of new points. But it is not easy to inspect the clustering by just looking at the printed labels. A visualization would be far more useful. We’ll inspect the clustering with a scatter plot!

Inspect clustering

Let’s now inspect the clustering we performed!

# Assign the columns of new_points: xs and ys
xs_np = new_points[:,0]
ys_np = new_points[:,1]

# Make a scatter plot of xs and ys, using labels to define the colors
_ = plt.scatter(xs_np, ys_np, c=labels_points, alpha=.5)

# Assign the cluster centers: centroids
centroids_p = model_points.cluster_centers_

# Assign the columns of centroids: centroids_x, centroids_y
centroids_x_p = centroids_p[:,0]
centroids_y_p = centroids_p[:,1]

# Make a scatter plot of centroids_x and centroids_y
_ = plt.scatter(centroids_x_p, centroids_y_p, marker="D", s=50)
plt.show()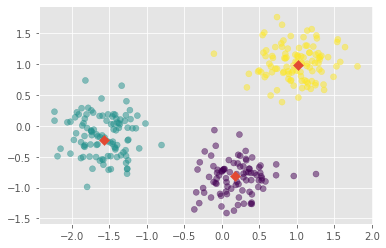

The clustering looks great! But how can we be sure that 3 clusters is the correct choice? In other words, how can we evaluate the quality of a clustering?

Evaluating a clustering

Can check correspondence with e.g. iris species
… but what if there are no species to check against?
Measure quality of a clustering
Informs choice of how many clusters to look for

Iris: clusters vs species

k-means found 3 clusters amongst the iris samples

Cross tabulation with pandas

Clusters vs species is a “cross-tabulation”

iris_ct = pd.DataFrame({'labels':labels_iris, 'species':iris.target})
iris_ct.head()

	labels	species
0	1	0
1	1	0
2	1	0
3	1	0
4	1	0

np.unique(iris.target)

array([0, 1, 2])

iris_ct.species.unique()

array([0, 1, 2])

iris.target_names

array(['setosa', 'versicolor', 'virginica'], dtype='<U10')

iris_ct['species'] = iris_ct.species.map({0:'setosa', 1:'versicolor', 2:'virginica'})
iris_ct.head()

	labels	species
0	1	setosa
1	1	setosa
2	1	setosa
3	1	setosa
4	1	setosa

Crosstab of labels and species

pd.crosstab(iris_ct.labels, iris_ct.species)

species	setosa	versicolor	virginica
labels
0	0	48	14
1	50	0	0
2	0	2	36

Measuring clustering quality

Using only samples and their cluster labels
A good clustering has tight clusters
… and samples in each cluster bunched together

Inertia measures clustering quality

Measures how spread out the clusters are (lower is better)

Distance from each sample to centroid of its cluster

After fit(), available as attribute inertia_

k-means attempts to minimize the inertia when choosing clusters

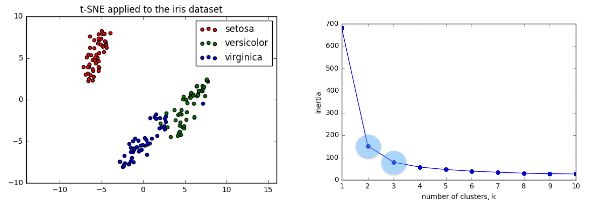
model.inertia_

78.851441426146

The number of clusters

Clusterings of the iris dataset with different numbers of clusters
More clusters means lower inertia
What is the best number of clusters?

How many clusters to choose?

A good clustering has tight clusters (so low inertia)
… but not too many clusters!
Choose an “elbow” in the inertia plot
Where inertia begins to decrease more slowly
E.g. for iris dataset, 3 is a good choice

How many clusters of grain?

samples_grain = pd.read_csv("datasets/samples_grain.csv").values
samples_grain[:5]

array([[15.26  , 14.84  ,  0.871 ,  5.763 ,  3.312 ,  2.221 ,  5.22  ],
       [14.88  , 14.57  ,  0.8811,  5.554 ,  3.333 ,  1.018 ,  4.956 ],
       [14.29  , 14.09  ,  0.905 ,  5.291 ,  3.337 ,  2.699 ,  4.825 ],
       [13.84  , 13.94  ,  0.8955,  5.324 ,  3.379 ,  2.259 ,  4.805 ],
       [16.14  , 14.99  ,  0.9034,  5.658 ,  3.562 ,  1.355 ,  5.175 ]])

an array samples contains the measurements (such as area, perimeter, length, and several others) of samples of grain. What’s a good number of clusters in this case?

ks_grain = range(1, 6)
inertias_grain = []

for k in ks_grain:
    # Create a KMeans instance with k clusters: model
    model_grain = KMeans(n_clusters=k)
    
    # Fit model to samples
    model_grain.fit(samples_grain)
    
    # Append the inertia to the list of inertias
    inertias_grain.append(model_grain.inertia_)
    
# Plot ks vs inertias
plt.plot(ks_grain, inertias_grain, '-o')
plt.xlabel('number of clusters, k')
plt.ylabel('inertia')
plt.xticks(ks_grain)
plt.show()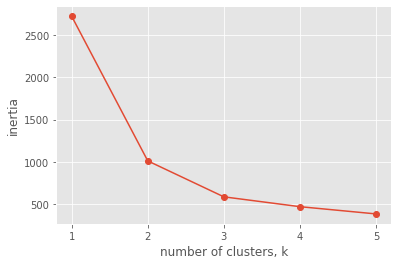

The inertia decreases very slowly from 3 clusters to 4, so it looks like 3 clusters would be a good choice for this data.

Evaluating the grain clustering

In fact, the grain samples come from a mix of 3 different grain varieties: “Kama”, “Rosa” and “Canadian”. We will cluster the grain samples into three clusters, and compare the clusters to the grain varieties using a cross-tabulation.

varieties = pd.read_csv("datasets/varieties.csv")["0"].to_list()
varieties[:5]

['Kama wheat', 'Kama wheat', 'Kama wheat', 'Kama wheat', 'Kama wheat']

list varieties gives the grain variety for each sample.

# Create a KMeans model with 3 clusters: model
model_grain = KMeans(n_clusters=3)

# Use fit_predict to fit model and obtain cluster labels: labels
labels_grain = model_grain.fit_predict(samples_grain)

# Create a DataFrame with labels and varieties as columns: df
grain_df = pd.DataFrame({'labels': labels_grain, 'varieties': varieties})

# Create crosstab: ct
ct_grain = pd.crosstab(grain_df.labels, grain_df.varieties)

# Display ct
ct_grain

varieties	Canadian wheat	Kama wheat	Rosa wheat
labels
0	0	1	60
1	2	60	10
2	68	9	0

The cross-tabulation shows that the 3 varieties of grain separate really well into 3 clusters. But depending on the type of data you are working with, the clustering may not always be this good. Is there anything we can do in such situations to improve the clustering?

Transforming features for better clusterings

Piedmont wines dataset {% fn 2 %}

178 samples from 3 distinct varieties of red wine: Barolo, Grignolino and Barbera

Features measure chemical composition e.g. alcohol content

… also visual properties like “color intensity”

Feature variancesfeature

The wine features have very different variances!

Variance of a feature measures spread of its values

StandardScaler

In kmeans: feature variance = feature influence

StandardScaler transforms each feature to have mean 0 and variance 1

Features are said to be “standardized”

Similar methods

StandardScaler and KMeans have similar methods

Use fit() / transform() with StandardScaler

Use fit() / predict() with KMeans

StandardScaler, then KMeans

Need to perform two steps: StandardScaler, then KMeans

Use sklearn pipeline to combine multiple steps

Data flows from one step into the next

sklearn preprocessing steps

StandardScaler is a “preprocessing” step

MaxAbsScaler and Normalizer are other examples

Scaling fish data for clustering

samples_fish = pd.read_csv("datasets/samples_fish.csv").values
samples_fish[:5]

array([[242. ,  23.2,  25.4,  30. ,  38.4,  13.4],
       [290. ,  24. ,  26.3,  31.2,  40. ,  13.8],
       [340. ,  23.9,  26.5,  31.1,  39.8,  15.1],
       [363. ,  26.3,  29. ,  33.5,  38. ,  13.3],
       [430. ,  26.5,  29. ,  34. ,  36.6,  15.1]])

an array samples_fish {% fn 3 %} gives measurements of fish. Each row represents an individual fish. The measurements, such as weight in grams, length in centimeters, and the percentage ratio of height to length, have very different scales. In order to cluster this data effectively, we’ll need to standardize these features first. We’ll build a pipeline to standardize and cluster the data.

# Create scaler: scaler_fish
scaler_fish = StandardScaler()

# Create KMeans instance: kmeans_fish
kmeans_fish = KMeans(n_clusters=4)

# Create pipeline: pipeline_fish
pipeline_fish = make_pipeline(scaler_fish, kmeans_fish)

Now that We’ve built the pipeline, we’ll use it to cluster the fish by their measurements.

Clustering the fish data

species_fish = pd.read_csv("datasets/species_fish.csv")["0"].to_list()
species_fish[:5]

['Bream', 'Bream', 'Bream', 'Bream', 'Bream']

We’ll now use the standardization and clustering pipeline to cluster the fish by their measurements, and then create a cross-tabulation to compare the cluster labels with the fish species.

# Fit the pipeline to samples
pipeline_fish.fit(samples_fish)

# Calculate the cluster labels: labels_fish
labels_fish = pipeline_fish.predict(samples_fish)

# Create a DataFrame with labels and species as columns: df
fish_df = pd.DataFrame({'labels':labels_fish, 'species':species_fish})

# Create crosstab: ct
ct_fish = pd.crosstab(fish_df.labels, fish_df.species)

# Display ct
ct_fish

species	Bream	Pike	Roach	Smelt
labels
0	33	0	1	0
1	1	0	19	1
2	0	17	0	0
3	0	0	0	13

It looks like the fish data separates really well into 4 clusters!

Clustering stocks using KMeans

We’ll cluster companies using their daily stock price movements (i.e. the dollar difference between the closing and opening prices for each trading day).

movements = pd.read_csv("datasets/movements.csv").values
movements[:5]

array([[  0.58    ,  -0.220005,  -3.409998, ...,  -5.359962,   0.840019,
        -19.589981],
       [ -0.640002,  -0.65    ,  -0.210001, ...,  -0.040001,  -0.400002,
          0.66    ],
       [ -2.350006,   1.260009,  -2.350006, ...,   4.790009,  -1.760009,
          3.740021],
       [  0.109997,   0.      ,   0.260002, ...,   1.849999,   0.040001,
          0.540001],
       [  0.459999,   1.77    ,   1.549999, ...,   1.940002,   1.130005,
          0.309998]])

A NumPy array movements of daily price movements from 2010 to 2015 (obtained from Yahoo! Finance), where each row corresponds to a company, and each column corresponds to a trading day.

Some stocks are more expensive than others. To account for this, we will include a Normalizer at the beginning of the pipeline. The Normalizer will separately transform each company’s stock price to a relative scale before the clustering begins.

Note

Normalizer() is different to StandardScaler(). While StandardScaler() standardizes features (such as the features of the fish data) by removing the mean and scaling to unit variance, Normalizer() rescales each sample - here, each company’s stock price - independently of the other.

# Create a normalizer: normalizer_movements
normalizer_movements = Normalizer()

# Create a KMeans model with 10 clusters: kmeans_movements
kmeans_movements = KMeans(n_clusters=10)

# Make a pipeline chaining normalizer and kmeans: pipeline_movements
pipeline_movements = make_pipeline(normalizer_movements, kmeans_movements)

# Fit pipeline to the daily price movements
pipeline_movements.fit(movements)

Pipeline(steps=[('normalizer', Normalizer()),
                ('kmeans', KMeans(n_clusters=10))])

Now that the pipeline has been set up, we can find out which stocks move together

Which stocks move together?

So which company have stock prices that tend to change in the same way? We’ll now inspect the cluster labels from the clustering to find out.

companies_movements=pd.read_csv("datasets/companies_movements.csv")
companies_movements.head()

	0
0	Apple
1	AIG
2	Amazon
3	American express
4	Boeing

companies_movements=companies_movements["0"].to_list()
companies_movements[:5]

['Apple', 'AIG', 'Amazon', 'American express', 'Boeing']

a list companies_movements of the company names

# Predict the cluster labels: labels_movements
labels_movements = pipeline_movements.predict(movements)

# Create a DataFrame aligning labels and companies: df
movements_df = pd.DataFrame({'labels': labels_movements, 'companies': companies_movements})

# Display df sorted by cluster label
movements_df.sort_values("labels")

	labels	companies
18	0	Goldman Sachs
26	0	JPMorgan Chase
16	0	General Electrics
15	0	Ford
5	0	Bank of America
55	0	Wells Fargo
3	0	American express
1	0	AIG
22	1	HP
20	1	Home Depot
58	1	Xerox
30	1	MasterCard
23	1	IBM
14	1	Dell
54	1	Walgreen
32	1	3M
11	1	Cisco
33	1	Microsoft
47	1	Symantec
8	1	Caterpillar
13	1	DuPont de Nemours
39	2	Pfizer
53	2	Valero Energy
37	2	Novartis
42	2	Royal Dutch Shell
6	2	British American Tobacco
57	2	Exxon
19	2	GlaxoSmithKline
35	2	Navistar
46	2	Sanofi-Aventis
52	2	Unilever
12	2	Chevron
10	2	ConocoPhillips
49	2	Total
43	2	SAP
44	2	Schlumberger
40	3	Procter Gamble
27	3	Kimberly-Clark
56	3	Wal-Mart
9	3	Colgate-Palmolive
25	3	Johnson & Johnson
2	4	Amazon
59	4	Yahoo
21	5	Honda
45	5	Sony
34	5	Mitsubishi
48	5	Toyota
7	5	Canon
24	6	Intel
50	6	Taiwan Semiconductor Manufacturing
51	6	Texas instruments
28	7	Coca Cola
31	7	McDonalds
41	7	Philip Morris
38	7	Pepsi
29	8	Lookheed Martin
4	8	Boeing
36	8	Northrop Grumman
17	9	Google/Alphabet
0	9	Apple

Visualization with hierarchical clustering and t-SNE

We’ll Explore two unsupervised learning techniques for data visualization, hierarchical clustering and t-SNE. Hierarchical clustering merges the data samples into ever-coarser clusters, yielding a tree visualization of the resulting cluster hierarchy. t-SNE maps the data samples into 2d space so that the proximity of the samples to one another can be visualized.

Visualizing hierarchies

Visualisations communicate insight

“t-SNE” : Creates a 2D map of a dataset (later)

“Hierarchical clustering”

A hierarchy of groups

Groups of living things can form a hierarchy

Clusters are contained in one another

Eurovision scoring dataset {% fn 4 %}

Countries gave scores to songs performed at the Eurovision 2016

2D array of scores

Rows are countries, columns are songs

Hierarchical clustering

Every country begins in a separate cluster

At each step, the two closest clusters are merged

Continue until all countries in a single cluster

This is “agglomerative” hierarchical clustering

The dendrogram of a hierarchical clustering

Read from the bottom up

Vertical lines represent clusters

With 5 data samples, there would be 4 merge operations, and with 6 data samples, there would be 5 merges, and so on.

Hierarchical clustering of the grain data

the SciPy linkage() function performs hierarchical clustering on an array of samples. We will use the linkage() function to obtain a hierarchical clustering of the grain samples, and use dendrogram() to visualize the result.

# Calculate the linkage: mergings_g
mergings_g = linkage(samples_grain, method='complete')

# Plot the dendrogram, using varieties as labels
plt.figure(figsize=(20,7))
dendrogram(mergings_g,
           labels=varieties,
           leaf_rotation=90,
           leaf_font_size=8,
)
plt.show()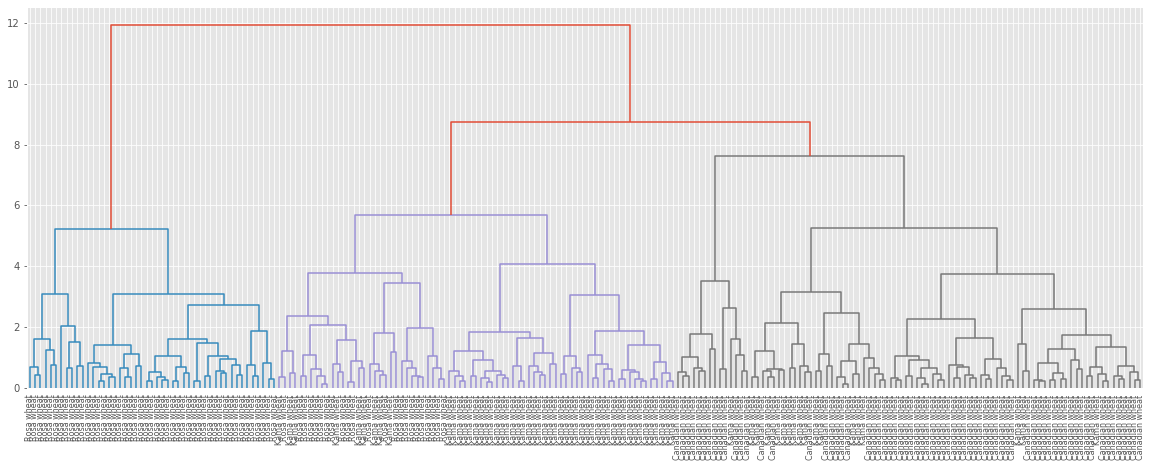

Dendrograms are a great way to illustrate the arrangement of the clusters produced by hierarchical clustering.

Hierarchies of stocks

We used k-means clustering to cluster companies according to their stock price movements. Now, we’ll perform hierarchical clustering of the companies. SciPy hierarchical clustering doesn’t fit into a sklearn pipeline, so we’ll need to use the normalize() function from sklearn.preprocessing instead of Normalizer.

# Normalize the movements: normalized_movements
normalized_movements = normalize(movements)

# Calculate the linkage: mergings
mergings_m = linkage(normalized_movements, method="complete")

# Plot the dendrogram
plt.figure(figsize=(20,10))
dendrogram(mergings_m, labels=companies_movements, leaf_font_size=12, leaf_rotation=90)
plt.show()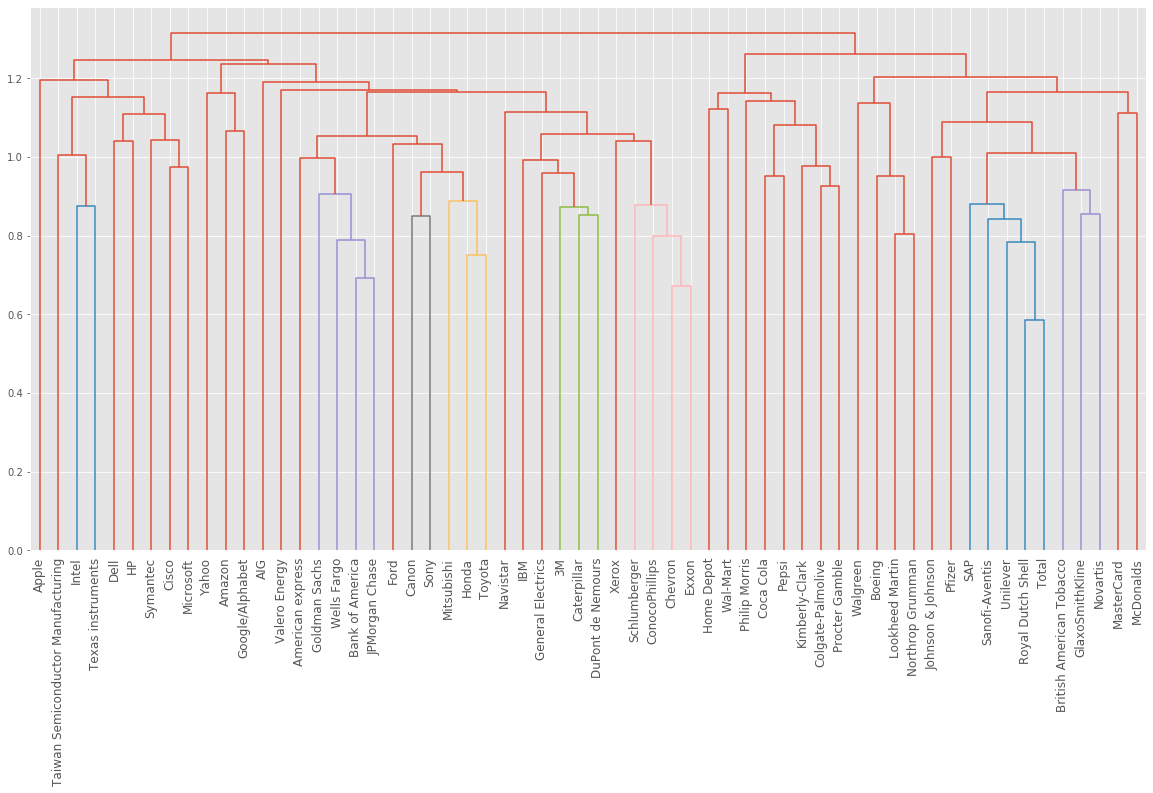

You can produce great visualizations such as this with hierarchical clustering, but it can be used for more than just visualizations.

Cluster labels in hierarchical clustering

Cluster labels in hierarchical clustering

Not only a visualisation tool!

Cluster labels at any intermediate stage can be recovered

For use in e.g. cross-tabulations

Intermediate clusterings & height on dendrogram

E.g. at height 15: Bulgaria, Cyprus, Greece are one cluster

Russia and Moldova are another

Armenia in a cluster on its own

Dendrograms show cluster distances

Height on dendrogram = distance between merging clusters

E.g. clusters with only Cyprus and Greece had distance approx. 6

This new cluster distance approx. 12 from cluster with only Bulgaria

Intermediate clusterings & height on dendrogram

Height on dendrogram specifies max. distance between merging clusters

Don’t merge clusters further apart than this (e.g. 15)

Distance between clusters

Defined by a “linkage method”

Specified via method parameter, e.g. linkage(samples, method=“complete”)

In “complete” linkage: distance between clusters is max. distance between their samples

Different linkage method, different hierarchical clustering!

Extracting cluster labels

Use the fcluster method

Returns a NumPy array of cluster labels

the linkage method defines how the distance between clusters is measured. In complete linkage, the distance between clusters is the distance between the furthest points of the clusters. In single linkage, the distance between clusters is the distance between the closest points of the clusters.

Different linkage, different hierarchical clustering!

We will perform a hierarchical clustering of the voting countries with ‘single’ linkage. Different linkage, different hierarchical clustering!

samples_eurovision = pd.read_csv("datasets/samples_eurovision.csv").values
samples_eurovision[:5]

array([[ 2., 12.,  0.,  0.,  0.,  8.,  0.,  0.,  0.,  0.,  0.,  0.,  1.,
         0., 10.,  0.,  4.,  0.,  5.,  7.,  0.,  0.,  3.,  0.,  6.,  0.],
       [12.,  0.,  4.,  0.,  0.,  0.,  0.,  6.,  0.,  7.,  8.,  0.,  3.,
         0.,  0.,  0.,  0.,  5.,  1., 12.,  0.,  0.,  2.,  0., 10.,  0.],
       [ 0., 12.,  3.,  0., 12., 10.,  0.,  0.,  0.,  7.,  0.,  0.,  0.,
         0.,  0.,  0.,  1.,  6.,  0.,  5.,  0.,  2.,  0.,  0.,  8.,  4.],
       [ 0.,  3., 12.,  0.,  0.,  5.,  0.,  0.,  0.,  1.,  0.,  2.,  0.,
         0.,  0.,  0.,  0.,  0., 12.,  8.,  4.,  0.,  7.,  6., 10.,  0.],
       [ 0.,  2.,  0., 12.,  0.,  8.,  0.,  0.,  0.,  4.,  1.,  0.,  7.,
         6.,  0.,  0.,  0.,  5.,  3., 12.,  0.,  0.,  0.,  0., 10.,  0.]])

country_names_eurovision = pd.read_csv("datasets/country_names_eurovision.csv")["0"].to_list()
country_names_eurovision[:5]

['Albania', 'Armenia', 'Australia', 'Austria', 'Azerbaijan']

len(country_names_eurovision)

# Calculate the linkage: mergings
mergings_ev = linkage(samples_eurovision, method='single')

# Plot the dendrogram
plt.figure(figsize=(20,9))
dendrogram(mergings_ev, labels=country_names_eurovision, leaf_rotation=90, leaf_font_size=12)
plt.show()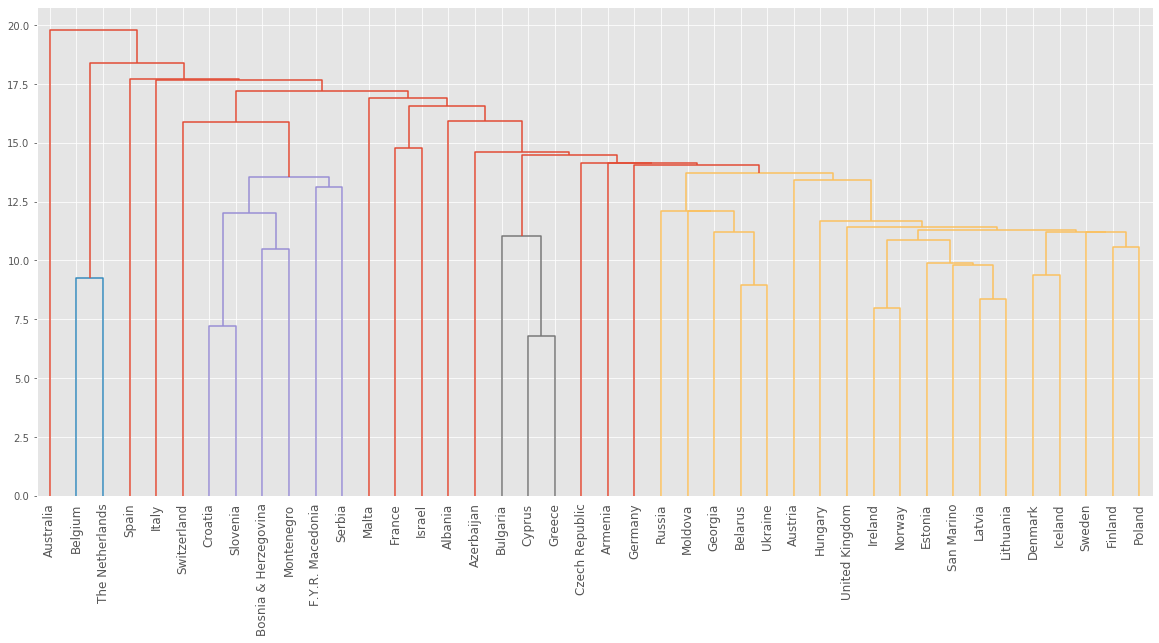

Extracting the cluster labels

We saw that the intermediate clustering of the grain samples at height 6 has 3 clusters. We will use the fcluster() function to extract the cluster labels for this intermediate clustering, and compare the labels with the grain varieties using a cross-tabulation.

# Use fcluster to extract labels: labels_g
labels_g = fcluster(mergings_g,6, criterion='distance')

# Create a DataFrame with labels and varieties as columns: df
grain_df = pd.DataFrame({'labels': labels_g, 'varieties': varieties})

# Create crosstab: ct
grain_ct = pd.crosstab(grain_df.labels, grain_df.varieties)

# Display ct
print(grain_ct)

varieties  Canadian wheat  Kama wheat  Rosa wheat
labels                                           
1                       0           0          47
2                       0          52          23
3                      13           1           0
4                      57          17           0

We’ve now mastered the fundamentals of k-Means and agglomerative hierarchical clustering. Next, we’ll explore t-SNE, which is a powerful tool for visualizing high dimensional data.

t-SNE for 2-dimensional maps

t-SNE for 2-dimensional maps

t-SNE = “t-distributed stochastic neighbor embedding”

Maps samples to 2D space (or 3D)

Map approximately preserves nearness of samples

Great for inspecting datasets

t-SNE on the iris dataset

Iris dataset has 4 measurements, so samples are 4-dimensional

t-SNE maps samples to 2D space

t-SNE didn’t know that there were different species

… yet kept the species mostly separate

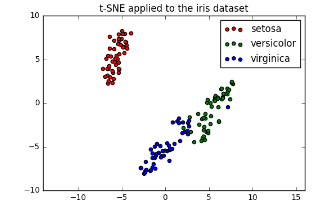
Interpreting t-SNE scatter plots

“versicolor” and “virginica” harder to distinguish from one another

Consistent with k-means inertia plot: could argue for 2 clusters, or for 3

t-SNE in sklearnIn

2D NumPy array samples

List species giving species of labels as number (0, 1, or 2)

samples[:5]

array([[5.1, 3.5, 1.4, 0.2],
       [4.9, 3. , 1.4, 0.2],
       [4.7, 3.2, 1.3, 0.2],
       [4.6, 3.1, 1.5, 0.2],
       [5. , 3.6, 1.4, 0.2]])

iris.target[:5]

array([0, 0, 0, 0, 0])

t-SNE in sklearn

model_i = TSNE(learning_rate=100)
transformed_i = model_i.fit_transform(samples)
xs_i = transformed_i[:,0]
ys_i = transformed_i[:,1]
plt.scatter(xs_i, ys_i, c=iris.target)
plt.show()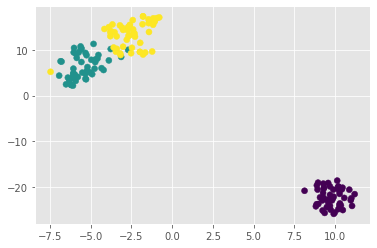

t-SNE has only fit_transform()

Has a fit_transform() method

Simultaneously fits the model and transforms the data

Has no separate fit() or transform() methods

Can’t extend the map to include new data samples

Must start over each time!

t-SNE learning rate

Choose learning rate for the dataset

Wrong choice: points bunch together

Try values between 50 and 200

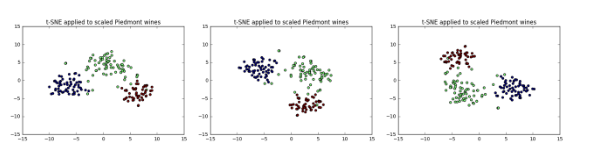
Different every time

t-SNE features are different every time

Piedmont wines, 3 runs, 3 different scatter plots!

… however: The wine varieties (=colors) have same position relative to one another

t-SNE visualization of grain dataset

We’ll apply t-SNE to the grain samples data and inspect the resulting t-SNE features using a scatter plot.

variety_numbers_g = pd.read_csv("datasets/variety_numbers_grains.csv")["0"].to_list()
variety_numbers_g[:5]

[1, 1, 1, 1, 1]

samples_grain[:5]

array([[15.26  , 14.84  ,  0.871 ,  5.763 ,  3.312 ,  2.221 ,  5.22  ],
       [14.88  , 14.57  ,  0.8811,  5.554 ,  3.333 ,  1.018 ,  4.956 ],
       [14.29  , 14.09  ,  0.905 ,  5.291 ,  3.337 ,  2.699 ,  4.825 ],
       [13.84  , 13.94  ,  0.8955,  5.324 ,  3.379 ,  2.259 ,  4.805 ],
       [16.14  , 14.99  ,  0.9034,  5.658 ,  3.562 ,  1.355 ,  5.175 ]])

# Create a TSNE instance: model
model_g = TSNE(learning_rate=200)

# Apply fit_transform to samples: tsne_features
tsne_features_g = model_g.fit_transform(samples_grain)

# Select the 0th feature: xs
xs_g = tsne_features_g[:,0]

# Select the 1st feature: ys
ys_g = tsne_features_g[:,1]

# Scatter plot, coloring by variety_numbers_g
plt.scatter(xs_g, ys_g, c=variety_numbers_g)
plt.show()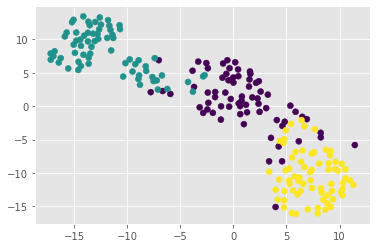

the t-SNE visualization manages to separate the 3 varieties of grain samples. But how will it perform on the stock data?

t-SNE map of the stock market

t-SNE provides great visualizations when the individual samples can be labeled. We’ll apply t-SNE to the company stock price data. A scatter plot of the resulting t-SNE features, labeled by the company names, gives a map of the stock market! The stock price movements for each company are available as the array normalized_movements. The list companies gives the name of each company.

# Create a TSNE instance: model
model_m = TSNE(learning_rate=50)

# Apply fit_transform to normalized_movements: tsne_features
tsne_features_m = model_m.fit_transform(normalized_movements)

# Select the 0th feature: xs
xs_m = tsne_features_m[:,0]

# Select the 1th feature: ys
ys_m = tsne_features_m[:,1]

# Scatter plot
plt.figure(figsize=(20,14))
plt.scatter(xs_m, ys_m)

# Annotate the points
for x, y, company in zip(xs_m, ys_m, companies_movements):
    plt.annotate(company, (x, y), fontsize=12)
plt.show()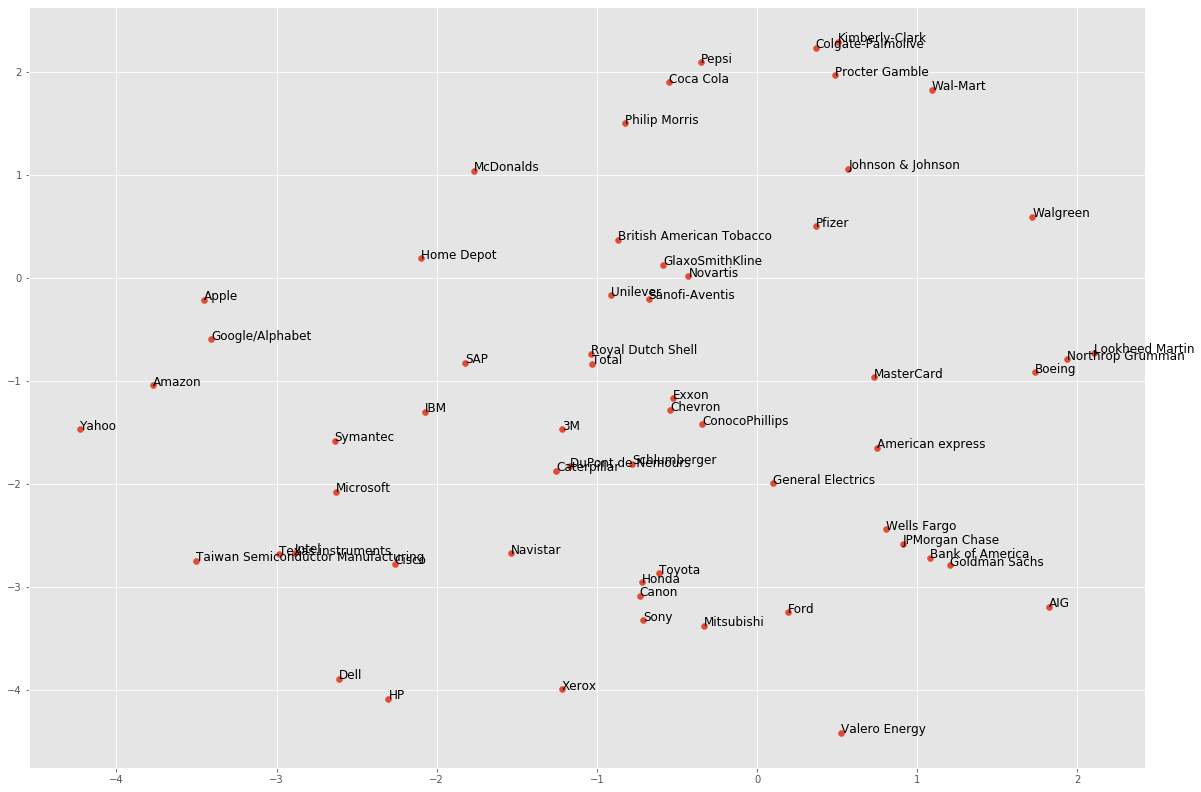

It’s visualizations such as this that make t-SNE such a powerful tool for extracting quick insights from high dimensional data.

Decorrelating the data and dimension reduction

Dimension reduction summarizes a dataset using its common occuring patterns. We’ll explore the most fundamental of dimension reduction techniques, “Principal Component Analysis” (“PCA”). PCA is often used before supervised learning to improve model performance and generalization. It can also be useful for unsupervised learning. For example, you’ll employ a variant of PCA will allow you to cluster Wikipedia articles by their content!

Visualizing the PCA transformation

Dimension reduction

More efficient storage and computation

Remove less-informative “noise” features

… which cause problems for prediction tasks, e.g. classification, regression

Principal Component Analysis

PCA = “Principal Component Analysis”

Fundamental dimension reduction technique

First step “decorrelation” (considered below)

Second step reduces dimension (considered later)

PCA aligns data with axes

Rotates data samples to be aligned with axes

Shifts data samples so they have mean 0

No information is lostPCA

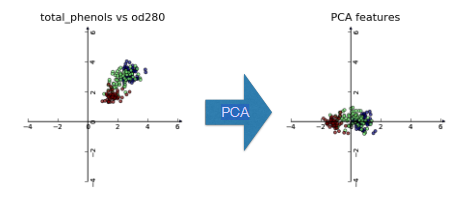
PCA follows the fit/transform pattern

PCA a scikit-learn component like KMeans or StandardScaler

fit() learns the transformation from given data

transform() applies the learned transformation

transform() can also be applied to new data

wine = pd.read_csv("datasets/wine.csv")
wine.head()

	class_label	class_name	alcohol	malic_acid	ash	alcalinity_of_ash	magnesium	total_phenols	flavanoids	nonflavanoid_phenols	proanthocyanins	color_intensity	hue	od280	proline
0	1	Barolo	14.23	1.71	2.43	15.6	127	2.80	3.06	0.28	2.29	5.64	1.04	3.92	1065
1	1	Barolo	13.20	1.78	2.14	11.2	100	2.65	2.76	0.26	1.28	4.38	1.05	3.40	1050
2	1	Barolo	13.16	2.36	2.67	18.6	101	2.80	3.24	0.30	2.81	5.68	1.03	3.17	1185
3	1	Barolo	14.37	1.95	2.50	16.8	113	3.85	3.49	0.24	2.18	7.80	0.86	3.45	1480
4	1	Barolo	13.24	2.59	2.87	21.0	118	2.80	2.69	0.39	1.82	4.32	1.04	2.93	735

Using scikit-learn PCA

samples_wine = array of two wine features (total_phenols & od280)

samples_wine = wine[['total_phenols', 'od280']].values
samples_wine[:5]

array([[2.8 , 3.92],
       [2.65, 3.4 ],
       [2.8 , 3.17],
       [3.85, 3.45],
       [2.8 , 2.93]])

model_w = PCA()
model_w.fit(samples_wine)

PCA()

transformed_w = model_w.transform(samples_wine)

PCA features

Rows of transformed correspond to samples

Columns of transformed are the “PCA features”

Row gives PCA feature values of corresponding sample

transformed_w[:5]

array([[nan, nan],
       [nan, nan],
       [nan, nan],
       [nan, nan],
       [nan, nan]])

PCA features are not correlated

Features of dataset are often correlated, e.g. total_phenols and od280

PCA aligns the data with axes

Resulting PCA features are not linearly correlated (“decorrelation”)PCA

Pearson correlation

Measures linear correlation of features

Value between -1 and 1

Value of 0 means no linear correlation

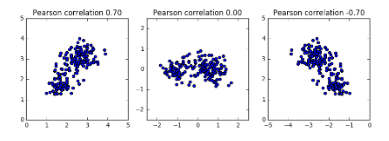
Principal components

“Principal components” = directions of variance

PCA aligns principal components with the axes

Available as components_ attribute of PCA object

Each row defines displacement from mean

model_w.components_

array([[nan, nan],
       [nan, nan]])

Correlated data in nature

We have array grains giving the width and length of samples of grain. We suspect that width and length will be correlated. To confirm this, let’s make a scatter plot of width vs length and measure their Pearson correlation.

# Assign the 0th column of grains: width
width_g = samples_grain[:,4]

# Assign the 1st column of grains: length
length_g = samples_grain[:,3]

# Scatter plot width vs length
plt.scatter(width_g, length_g)
plt.axis('equal')
plt.show()

# Calculate the Pearson correlation
correlation_g, pvalue_g = pearsonr(width_g, length_g)

# Display the correlation
correlation_g

0.8604149377143469

As you would expect, the width and length of the grain samples are highly correlated.

Decorrelating the grain measurements with PCA

We observed that the width and length measurements of the grain are correlated. Now, we’ll use PCA to decorrelate these measurements, then plot the decorrelated points and measure their Pearson correlation.

grains = pd.read_csv("datasets/grains.csv").values
grains[:5]

array([[3.312, 5.763],
       [3.333, 5.554],
       [3.337, 5.291],
       [3.379, 5.324],
       [3.562, 5.658]])

# Create PCA instance: model_g
model_g = PCA()

# Apply the fit_transform method of model to grains: pca_features
pca_features_g = model_g.fit_transform(grains)

# Assign 0th column of pca_features: xs
xs_g = pca_features_g[:,0]

# Assign 1st column of pca_features: ys
ys_g = pca_features_g[:,1]

# Scatter plot xs vs ys
plt.scatter(xs_g, ys_g)
plt.axis('equal')
plt.show()

# Calculate the Pearson correlation of xs and ys
correlation_g, pvalue_g = pearsonr(xs_g, ys_g)

# Display the correlation
correlation_g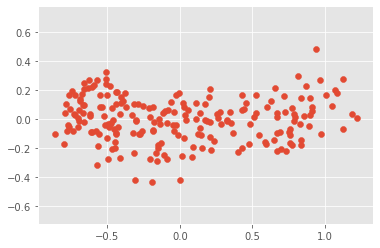

1.5634195327240974e-16

principal components have to align with the axes of the point cloud.

Intrinsic dimension

Intrinsic dimension of a flight path

2 features: longitude and latitude at points along a flight path

Dataset appears to be 2-dimensional

But can approximate using one feature: displacement along flight path

Is intrinsically 1-dimensiona

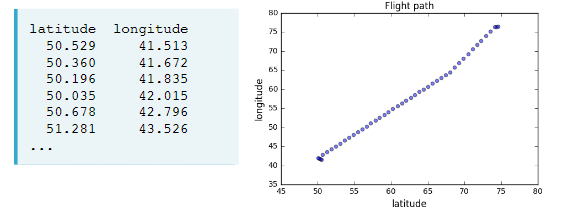
Intrinsic dimension

Intrinsic dimension = number of features needed to approximate the dataset

Essential idea behind dimension reduction

What is the most compact representation of the samples?

Can be detected with PCA

Versicolor dataset

“versicolor”, one of the iris species

Only 3 features: sepal length, sepal width, and petal width

Samples are points in 3D space

Versicolor dataset has intrinsic dimension 2

Samples lie close to a flat 2-dimensional sheet

So can be approximated using 2 features

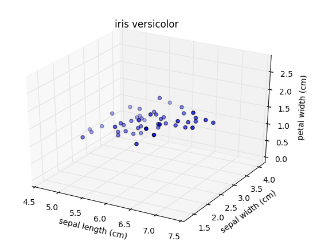
PCA identifies intrinsic dimension

Scatter plots work only if samples have 2 or 3 features

PCA identifies intrinsic dimension when samples have any number of features

Intrinsic dimension = number of PCA features with significant variance

PCA of the versicolor samples

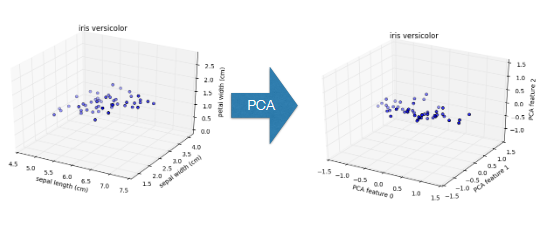
PCA features are ordered by variance descending

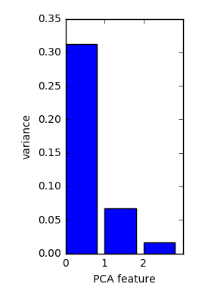
Variance and intrinsic dimension

Intrinsic dimension is number of PCA features with significant variance

In our example: the first two PCA features

So intrinsic dimension is 2

iris.target_names

array(['setosa', 'versicolor', 'virginica'], dtype='<U10')

versicolor = pd.DataFrame(iris.data, columns=iris.feature_names)
versicolor['target'] = iris.target
versicolor = versicolor[versicolor.target==1]
versicolor.head()

	sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)	target
50	7.0	3.2	4.7	1.4	1
51	6.4	3.2	4.5	1.5	1
52	6.9	3.1	4.9	1.5	1
53	5.5	2.3	4.0	1.3	1
54	6.5	2.8	4.6	1.5	1

samples_versicolor = versicolor[['sepal length (cm)', 'sepal width (cm)', 'petal width (cm)']].values
samples_versicolor[:5]

array([[7. , 3.2, 1.4],
       [6.4, 3.2, 1.5],
       [6.9, 3.1, 1.5],
       [5.5, 2.3, 1.3],
       [6.5, 2.8, 1.5]])

Plotting the variances of PCA features

samples_versicolor = array of versicolor samples

pca_versicolor = PCA()
pca_versicolor.fit(samples_versicolor)

PCA()

features_versicolor = range(pca_versicolor.n_components_)
plt.bar(features_versicolor, pca_versicolor.explained_variance_)
plt.xticks(features_versicolor)
plt.xlabel("PCA feature")
plt.ylabel("Variance")
plt.show()

Intrinsic dimension can be ambiguous

Intrinsic dimension is an idealization

… there is not always one correct answer!

Piedmont wines: could argue for 2, or for 3, or more

The first principal component

The first principal component of the data is the direction in which the data varies the most. We will use PCA to find the first principal component of the length and width measurements of the grain samples, and represent it as an arrow on the scatter plot.

# Make a scatter plot of the untransformed points
plt.scatter(grains[:,0], grains[:,1])

# Fit model to points
model_g.fit(grains)

# Get the mean of the grain samples: mean
mean_g = model_g.mean_

# Get the first principal component: first_pc
first_pc_g = model_g.components_[0,:]

# Plot first_pc as an arrow, starting at mean
plt.arrow(mean_g[0], mean_g[1], first_pc_g[0], first_pc_g[1], color='blue', width=0.01)

# Keep axes on same scale
plt.axis('equal')
plt.show()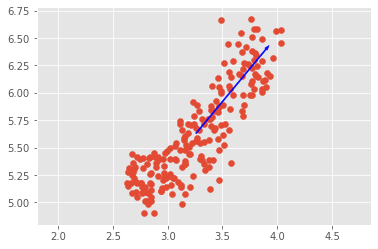

This is the direction in which the grain data varies the most.

Variance of the PCA features

The fish dataset is 6-dimensional. But what is its intrinsic dimension? We will make a plot of the variances of the PCA features to find out. We’ll need to standardize the features first.

# Create scaler: scaler
scaler_fish = StandardScaler()

# Create a PCA instance: pca
pca_fish = PCA()

# Create pipeline: pipeline
pipeline_fish = make_pipeline(scaler_fish, pca_fish)

# Fit the pipeline to 'samples'
pipeline_fish.fit(samples_fish)

# Plot the explained variances
features_fish = range(pca_fish.n_components_)
plt.bar(features_fish, pca_fish.explained_variance_)
plt.xlabel('PCA feature')
plt.ylabel('variance')
plt.xticks(features_fish)
plt.show()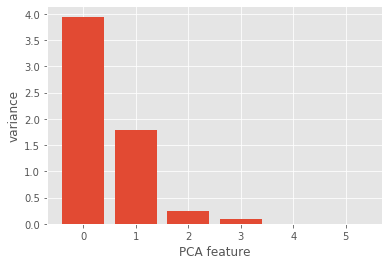

It looks like PCA features 0 and 1 have significant variance. Since PCA features 0 and 1 have significant variance, the intrinsic dimension of this dataset appears to be 2.

Dimension reduction with PCA

Dimension reduction

Represents same data, using less features

Important part of machine-learning pipelines

Can be performed using PCA

Dimension reduction with PCA

PCA features are in decreasing order of variance

Assumes the low variance features are “noise”

… and high variance features are informative

Dimension reduction with PCA

Specify how many features to keep

E.g. PCA(n_components=2)

Keeps the first 2 PCA features

Intrinsic dimension is a good choice

Dimension reduction of iris dataset

samples = array of iris measurements (4 features)

species = list of iris species numbers

Dimension reduction with PCA

Discards low variance PCA features

Assumes the high variance features are informative

Assumption typically holds in practice (e.g. for iris)

Word frequency arrays

Rows represent documents, columns represent words

Entries measure presence of each word in each document

… measure using “tf-idf” (more later)

Sparse arrays and csr_matrix

Array is “sparse”: most entries are zero

Can use scipy.sparse.csr_matrix instead of NumPy array

csr_matrix remembers only the non-zero entries (saves space!)

TruncatedSVD and csr_matrix

scikit-learn PCA doesn’t support csr_matrix

Use scikit-learn TruncatedSVD instead

Performs same transformation

Dimension reduction of the fish measurements

We saw that 2 was a reasonable choice for the “intrinsic dimension” of the fish measurements. We will use PCA for dimensionality reduction of the fish measurements, retaining only the 2 most important components.

scaled_samples_fish = pd.read_csv("datasets/scaled_samples_fish.csv").values
scaled_samples_fish[:5]

array([[-0.50109735, -0.36878558, -0.34323399, -0.23781518,  1.0032125 ,
         0.25373964],
       [-0.37434344, -0.29750241, -0.26893461, -0.14634781,  1.15869615,
         0.44376493],
       [-0.24230812, -0.30641281, -0.25242364, -0.15397009,  1.13926069,
         1.0613471 ],
       [-0.18157187, -0.09256329, -0.04603648,  0.02896467,  0.96434159,
         0.20623332],
       [-0.00464454, -0.0747425 , -0.04603648,  0.06707608,  0.8282934 ,
         1.0613471 ]])

# Create a PCA model with 2 components: pca
pca_fish = PCA(n_components=2)

# Fit the PCA instance to the scaled samples
pca_fish.fit(scaled_samples_fish)

# Transform the scaled samples: pca_features
pca_features_fish = pca_fish.transform(scaled_samples_fish)

# Print the shape of pca_features
pca_features_fish.shape

(85, 2)

We’ve successfully reduced the dimensionality from 6 to 2.

A tf-idf word-frequency array

We’ll create a tf-idf word frequency array for a toy collection of documents. For this, we will use the TfidfVectorizer from sklearn. It transforms a list of documents into a word frequency array, which it outputs as a csr_matrix. It has fit() and transform() methods like other sklearn objects.

documents = ['cats say meow', 'dogs say woof', 'dogs chase cats']

# Create a TfidfVectorizer: tfidf
tfidf_d = TfidfVectorizer() 

# Apply fit_transform to document: csr_mat
csr_mat_d = tfidf_d.fit_transform(documents)

# Print result of toarray() method
print(csr_mat_d.toarray())

# Get the words: words
words_d = tfidf_d.get_feature_names()

# Print words
words_d

[[0.51785612 0.         0.         0.68091856 0.51785612 0.        ]
 [0.         0.         0.51785612 0.         0.51785612 0.68091856]
 [0.51785612 0.68091856 0.51785612 0.         0.         0.        ]]

['cats', 'chase', 'dogs', 'meow', 'say', 'woof']

Clustering Wikipedia part I

TruncatedSVD is able to perform PCA on sparse arrays in csr_matrix format, such as word-frequency arrays. We will cluster some popular pages from Wikipedia {% fn 5 %}. We will build the pipeline and apply it to the word-frequency array of some Wikipedia articles.

The Pipeline object will be consisting of a TruncatedSVD followed by KMeans.

# Create a TruncatedSVD instance: svd
svd_wp = TruncatedSVD(n_components=50)

# Create a KMeans instance: kmeans
kmeans_wp = KMeans(n_clusters=6)

# Create a pipeline: pipeline
pipeline_wp = make_pipeline(svd_wp, kmeans_wp)

Now that we have set up the pipeline, we will use to cluster the articles.

Clustering Wikipedia part II

wv = pd.read_csv("datasets/Wikipedia_articles/wikipedia-vectors.csv", index_col=0)
articles = csr_matrix(wv.transpose())
articles_titles = list(wv.columns)

# Fit the pipeline to articles
pipeline_wp.fit(articles)

# Calculate the cluster labels: labels
labels_wp = pipeline_wp.predict(articles)

# Create a DataFrame aligning labels and titles: df
wp = pd.DataFrame({'label': labels_wp, 'article': articles_titles})

# Display df sorted by cluster label
wp.sort_values("label")

	label	article
47	0	Fever
40	0	Tonsillitis
41	0	Hepatitis B
42	0	Doxycycline
43	0	Leukemia
44	0	Gout
45	0	Hepatitis C
46	0	Prednisone
49	0	Lymphoma
48	0	Gabapentin
58	1	Sepsis
59	1	Adam Levine
50	1	Chad Kroeger
51	1	Nate Ruess
52	1	The Wanted
53	1	Stevie Nicks
54	1	Arctic Monkeys
55	1	Black Sabbath
56	1	Skrillex
57	1	Red Hot Chili Peppers
28	2	Anne Hathaway
27	2	Dakota Fanning
26	2	Mila Kunis
25	2	Russell Crowe
29	2	Jennifer Aniston
23	2	Catherine Zeta-Jones
22	2	Denzel Washington
21	2	Michael Fassbender
20	2	Angelina Jolie
24	2	Jessica Biel
10	3	Global warming
11	3	Nationally Appropriate Mitigation Action
12	3	Nigel Lawson
13	3	Connie Hedegaard
14	3	Climate change
15	3	Kyoto Protocol
17	3	Greenhouse gas emissions by the United States
18	3	2010 United Nations Climate Change Conference
16	3	350.org
19	3	2007 United Nations Climate Change Conference
9	4	LinkedIn
1	4	Alexa Internet
2	4	Internet Explorer
3	4	HTTP cookie
4	4	Google Search
5	4	Tumblr
6	4	Hypertext Transfer Protocol
7	4	Social search
8	4	Firefox
0	4	HTTP 404
30	5	France national football team
31	5	Cristiano Ronaldo
32	5	Arsenal F.C.
33	5	Radamel Falcao
34	5	Zlatan Ibrahimović
35	5	Colombia national football team
36	5	2014 FIFA World Cup qualification
37	5	Football
38	5	Neymar
39	5	Franck Ribéry

Discovering interpretable features

We’ll explore a dimension reduction technique called “Non-negative matrix factorization” (“NMF”) that expresses samples as combinations of interpretable parts. For example, it expresses documents as combinations of topics, and images in terms of commonly occurring visual patterns. We’ll also explore how to use NMF to build recommender systems that can find us similar articles to read, or musical artists that match your listening history!

Non-negative matrix factorization (NMF)

NMF = “non-negative matrix factorization”
Dimension reduction technique
NMF models are interpretable (unlike PCA)
Easy to interpret means easy to explain!
However, all sample features must be non-negative (>= 0)

Interpretable parts

NMF expresses documents as combinations of topics (or “themes”)

NMF expresses images as combinations of patterns

Using scikit-learn NMF

Follows fit() / transform() pattern

Must specify number of components e.g. NMF(n_components=2)

Works with NumPy arrays and with csr_matrix

Example word-frequency array

Word frequency array, 4 words, many documents

Measure presence of words in each document using “tf-idf”

“tf” = frequency of word in document

“idf” reduces influence of frequent words

NMF components

NMF has components

… just like PCA has principal components

Dimension of components = dimension of samples

Entries are non-negative

NMF features

NMF feature values are non-negative

Can be used to reconstruct the samples

… combine feature values with components

Sample reconstruction

Multiply components by feature values, and add up

Can also be expressed as a product of matrices

This is the “Matrix Factorization” in “NMF”

NMF fits to non-negative data, only

Word frequencies in each document

Images encoded as arrays

Audio spectrograms

Purchase histories on e-commerce sites

… and many more!

Non-negative data

A tf-idf word-frequency array.
An array where rows are customers, columns are products and entries are 0 or 1, indicating whether a customer has purchased a product.

NMF applied to Wikipedia articles

# Create an NMF instance: model
model_wp = NMF(n_components=6)

# Fit the model to articles
model_wp.fit(articles)

# Transform the articles: nmf_features
nmf_features_wp = model_wp.transform(articles)

# Print the NMF features
nmf_features_wp[:5]

array([[0.        , 0.        , 0.        , 0.        , 0.        ,
        0.44041429],
       [0.        , 0.        , 0.        , 0.        , 0.        ,
        0.56653905],
       [0.00382072, 0.        , 0.        , 0.        , 0.        ,
        0.39860038],
       [0.        , 0.        , 0.        , 0.        , 0.        ,
        0.3816956 ],
       [0.        , 0.        , 0.        , 0.        , 0.        ,
        0.48546058]])

NMF features of the Wikipedia articles

Note

When investigating the features, notice that for both actors, the NMF feature 3 has by far the highest value. This means that both articles are reconstructed using mainly the 3rd NMF component. We’ll see why: NMF components represent topics (for instance, acting!).

# Create a pandas DataFrame: df
wp_df = pd.DataFrame(nmf_features_wp, index=articles_titles)

# Print the row for 'Anne Hathaway'
display(wp_df.loc[['Anne Hathaway']])

# Print the row for 'Denzel Washington'
display(wp_df.loc[['Denzel Washington']])

	0	1	2	3	4	5
Anne Hathaway	0.003846	0.0	0.0	0.575735	0.0	0.0

	0	1	2	3	4	5
Denzel Washington	0.0	0.005601	0.0	0.422398	0.0	0.0

NMF learns interpretable parts

Example: NMF learns interpretable parts

Word-frequency array articles (tf-idf )

20,000 scientific articles (rows)

800 words (columns)

articles.shape

(60, 13125)

NMF components are topics

NMF components

For documents:

NMF components represent topics

NMF features combine topics into documents

For images, NMF components are parts of images

Grayscale images

“Grayscale” image = no colors, only shades of gray

Measure pixel brightness

Represent with value between 0 and 1 (0 is black)

Convert to 2D array

Encoding a collection of images

Collection of images of the same size

Encode as 2D array

Each row corresponds to an image

Each column corresponds to a pixel

… can apply NMF!

NMF learns topics of documents

when NMF is applied to documents, the components correspond to topics of documents, and the NMF features reconstruct the documents from the topics. We will using the NMF model that we built earlier using the Wikipedia articles. 3rd NMF feature value was high for the articles about actors Anne Hathaway and Denzel Washington. We will identify the topic of the corresponding NMF component.

words = pd.read_csv("datasets/Wikipedia_articles/words.csv")["0"].to_list()
words[:5]

['aaron', 'abandon', 'abandoned', 'abandoning', 'abandonment']

# Create a DataFrame: components_df
components_df = pd.DataFrame(model_wp.components_, columns=words)

# Print the shape of the DataFrame
print(components_df.shape)

# Select row 3: component
component = components_df.iloc[3]

# Print result of nlargest
component.nlargest()

(6, 13125)

film       0.627850
award      0.253121
starred    0.245274
role       0.211442
actress    0.186390
Name: 3, dtype: float64

Explore the LED digits dataset

We’ll use NMF to decompose grayscale images into their commonly occurring patterns. Firstly, we’ll explore the image dataset and see how it is encoded as an array.

samples_images = pd.read_csv("datasets/samples_images.csv")
x=samples_images.isnull().sum()
x[x>0]

Series([], dtype: int64)

samples_images=samples_images.values
np.isinf(samples_images).any()

False

np.isnan(samples_images).any()

False

# Select the 0th row: digit
digit_i = samples_images[0,:]

# Print digit
print(digit_i)

# Reshape digit to a 13x8 array: bitmap
bitmap_i = digit_i.reshape(13,8)

# Print bitmap
print(bitmap_i)

# Use plt.imshow to display bitmap
plt.imshow(bitmap_i, cmap='gray', interpolation='nearest')
plt.colorbar()
plt.show()

[0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 1. 1. 1. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0.
 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 1. 0.
 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 1. 0.
 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0.
 0. 0. 0. 0. 0. 0. 0. 0.]
[[0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 1. 1. 1. 1. 0. 0.]
 [0. 0. 0. 0. 0. 0. 1. 0.]
 [0. 0. 0. 0. 0. 0. 1. 0.]
 [0. 0. 0. 0. 0. 0. 1. 0.]
 [0. 0. 0. 0. 0. 0. 1. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 1. 0.]
 [0. 0. 0. 0. 0. 0. 1. 0.]
 [0. 0. 0. 0. 0. 0. 1. 0.]
 [0. 0. 0. 0. 0. 0. 1. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0.]]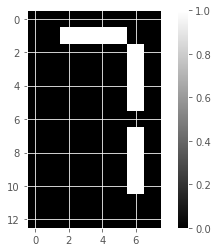

NMF learns the parts of images

def show_as_image(sample):
    """displays the image encoded by any 1D array"""
    bitmap = sample.reshape((13, 8))
    plt.figure()
    plt.imshow(bitmap, cmap='gray', interpolation='nearest')
    plt.colorbar()
    plt.show()

show_as_image(samples_images[99, :])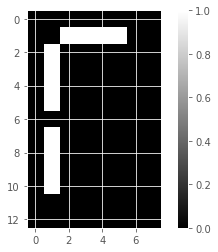

# Create an NMF model: model
model_i = NMF(n_components=7)

# Apply fit_transform to samples: features
features_i = model_i.fit_transform(samples_images)

# Call show_as_image on each component
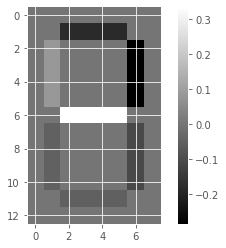
for component in model_i.components_:
    show_as_image(component)

# Assign the 0th row of features: digit_features
digit_features_i = features_i[0,:]

# Print digit_features
digit_features_i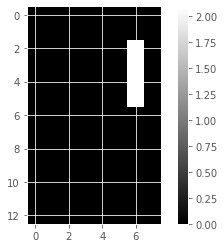

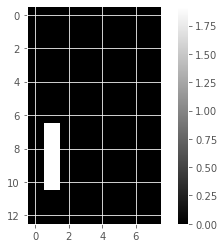
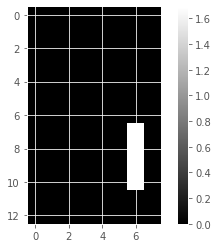
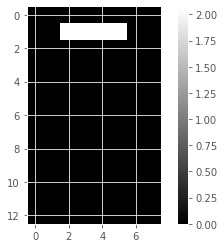
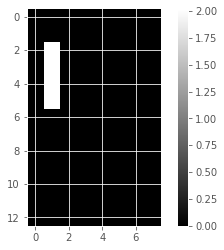
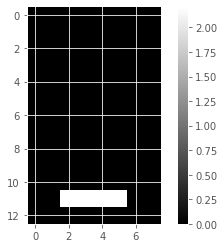
array([4.76823559e-01, 0.00000000e+00, 0.00000000e+00, 5.90605054e-01,
       4.81559442e-01, 0.00000000e+00, 7.37535093e-16])

PCA doesn’t learn parts

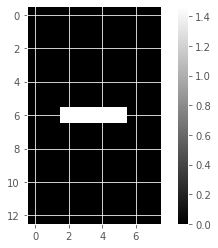
Unlike NMF, PCA doesn’t learn the parts of things. Its components do not correspond to topics (in the case of documents) or to parts of images, when trained on images. We will verify by inspecting the components of a PCA model fit to the dataset of LED digit images

# Create a PCA instance: model
model_i = PCA(n_components=7)

# Apply fit_transform to samples: features
features_i = model_i.fit_transform(samples_images)

# Call show_as_image on each component
for component in model_i.components_:
    show_as_image(component)

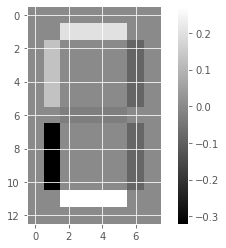
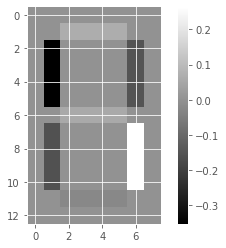
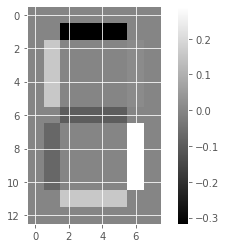
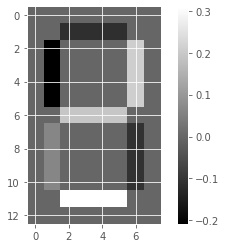
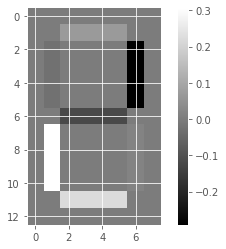
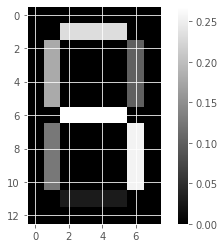
the components of PCA do not represent meaningful parts of images of LED digits!

Building recommender systems using NMF

Finding similar articles

Engineer at a large online newspaper

Task: recommend articles similar to article being read by customer

Similar articles should have similar topics

Strategy

Apply NMF to the word-frequency array

NMF feature values describe the topics

… so similar documents have similar NMF feature values

Compare NMF feature values?

Versions of articles

Different versions of the same document have same topic proportions

… exact feature values may be different!

E.g. because one version uses many meaningless words

But all versions lie on the same line through the origin

Cosine similarity

Uses the angle between the lines

Higher values means more similar

Maximum value is 1, when angle is 0

Which articles are similar to ‘Cristiano Ronaldo’?

finding the articles most similar to the article about the footballer Cristiano Ronaldo.

# Normalize the NMF features: norm_features
norm_features_wp = normalize(nmf_features_wp)

# Create a DataFrame: df
wp_df = pd.DataFrame(norm_features_wp, index=articles_titles)

# Select the row corresponding to 'Cristiano Ronaldo': article
article = wp_df.loc['Cristiano Ronaldo']

# Compute the dot products: similarities
similarities = wp_df.dot(article)

# Display those with the largest cosine similarity
similarities.nlargest()

Cristiano Ronaldo                1.000000
Franck Ribéry                    0.999972
Radamel Falcao                   0.999942
Zlatan Ibrahimović               0.999942
France national football team    0.999923
dtype: float64

Recommend musical artists part I

recommend popular music artists!

artists_df = pd.read_csv("datasets/Musical_artists/scrobbler-small-sample.csv")
artists = csr_matrix(artists_df)

# Create a MaxAbsScaler: scaler
scaler = MaxAbsScaler()

# Create an NMF model: nmf
nmf = NMF(n_components=20)

# Create a Normalizer: normalizer
normalizer = Normalizer()

# Create a pipeline: pipeline
pipeline = make_pipeline(scaler, nmf, normalizer)

# Apply fit_transform to artists: norm_features
norm_features = pipeline.fit_transform(artists)

Recommend musical artists part II

Suppose you were a big fan of Bruce Springsteen - which other musicial artists might you like? We will use the NMF features and the cosine similarity to find similar musical artists.

artist_names = pd.read_csv("datasets/Musical_artists/artists.csv")["0"].to_list()

# Create a DataFrame: df
df = pd.DataFrame(norm_features, index=artist_names)

# Select row of 'Bruce Springsteen': artist
artist = df.loc['Bruce Springsteen']

# Compute cosine similarities: similarities
similarities = df.dot(artist)

# Display those with highest cosine similarity
similarities.nlargest()

ValueError: Shape of passed values is (2894, 20), indices imply (111, 20)

{{ ‘Source: http://scikit-learn.org/stable/modules/generated/sklearn.datasets.load_iris.html.’ | fndetail: 1 }} {{ ‘Source: https://archive.ics.uci.edu/ml/datasets/Wine.’ | fndetail: 2 }} {{ ‘These fish measurement data were sourced from the Journal of Statistics Education..’ | fndetail: 3 }} {{ ‘Source: http://www.eurovision.tv/page/results’ | fndetail: 4 }} {{ ‘The Wikipedia dataset you will be working with was obtained from here.’ | fndetail: 5 }}

Overview

Libraries

Clustering for dataset exploration

Unsupervised Learning

Unsupervised learning

Supervised vs unsupervised learning

Iris dataset

Iris data is 4-dimensional

k-means clustering

Cluster labels for new samples

Scatter plots

k-means clustering with scikit-learn

Cluster labels for new samples

Scatter plots

Clustering 2D points

Inspect clustering

Evaluating a clustering

Iris: clusters vs species

Cross tabulation with pandas

Crosstab of labels and species

Measuring clustering quality

Inertia measures clustering quality

The number of clusters

How many clusters to choose?

How many clusters of grain?

Evaluating the grain clustering

Transforming features for better clusterings

Piedmont wines dataset {% fn 2 %}

Feature variancesfeature

StandardScaler

Similar methods

StandardScaler, then KMeans

sklearn preprocessing steps

Scaling fish data for clustering

Clustering the fish data

Clustering stocks using KMeans

Which stocks move together?

Visualization with hierarchical clustering and t-SNE

Visualizing hierarchies

Visualisations communicate insight

A hierarchy of groups

Eurovision scoring dataset {% fn 4 %}

Hierarchical clustering

The dendrogram of a hierarchical clustering

Hierarchical clustering of the grain data

Hierarchies of stocks

Cluster labels in hierarchical clustering

Cluster labels in hierarchical clustering

Intermediate clusterings & height on dendrogram

Dendrograms show cluster distances

Intermediate clusterings & height on dendrogram

Distance between clusters

Extracting cluster labels

Different linkage, different hierarchical clustering!

Extracting the cluster labels

t-SNE for 2-dimensional maps

t-SNE for 2-dimensional maps

t-SNE on the iris dataset

Interpreting t-SNE scatter plots

t-SNE in sklearnIn

t-SNE in sklearn

t-SNE has only fit_transform()

t-SNE learning rate

Different every time

t-SNE visualization of grain dataset

t-SNE map of the stock market

Decorrelating the data and dimension reduction

Visualizing the PCA transformation

Dimension reduction

Principal Component Analysis

PCA aligns data with axes

PCA follows the fit/transform pattern

Using scikit-learn PCA

PCA features

PCA features are not correlated

Pearson correlation

Principal components

Correlated data in nature

Decorrelating the grain measurements with PCA

Intrinsic dimension

`StandardScaler`, then `KMeans`

t-SNE has only `fit_transform()`